Kalypso
List of Products
Kalypso 1D/2D
is a module for computing unsteady coupled 1D/2D flows for surface waters. Coupling in this context refers to a serial coupling of models, thus enabling to connect a one-dimensionally modeled river section with another section which has been modeled using the 2D model. Both models will be simulated integrally, boundary conditions will be automatically shared between the two models. The standard version supports the computation module from the Institute of Hydraulic Engineering at the Technical University of Hamburg-Harburg. The program nucleus is based on RMA 10s by Dr. Ian King and has been further enhanced by the Technical University of Hamburg-Harburg since 2005. This computation module is currently not by default distributed with the Kalypso modules.
The mathematical basis of the computation module is formed by the St. Venant equations and the depth-averaged shallow water equations, respectively. The computation module is based on the finite element method. A modified Crank-Nicolson time-stepping scheme is used to advance the solution in time; the nonlinear equations are solved using the iterative Newton-Raphson method.
Main features of the computation module are
- Optional use of the flow laws of DARCY-WEISBACH or GAUCKLER-MANNING-STRICKLER,
- Consideration of fouling roughness according to PASCHE,
- Turbulence model (2D): constant eddy viscosity, soil surface induced turbulence model, Prandtls’ mixing length concept and Smagorinskys’ model,
- Wetting and drying algorithms (2D),
- Computation of subcritical and supercritical flows.
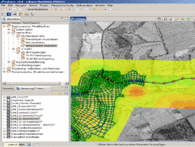
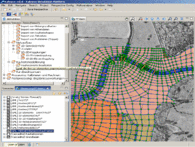
Graphical user interface
- Finite element mesh generator
- Finite element mesh generator for river channels on the basis of cross sections
- Assignment of elevations to finite element nodal points on the basis of digital terrain model data (BCE HMO, ESRI ASCII Grid)
- Assignment of roughness zones to finite elements on the basis of land use data
- Automatic GIS-based analysis of computation module results (e.g. flow vectors, isolines and -areas)
- Generation of hydrographs at user defined finite element nodal points
- Generation of arbitrary user defined cross sections of the finite element model